
The other formulas provided are usually more useful and represent the most common situations that physicists run into. It comes naturally from what we just learned about rotation. We have a comprehensive article explaining the approach to solving the moment of inertia.
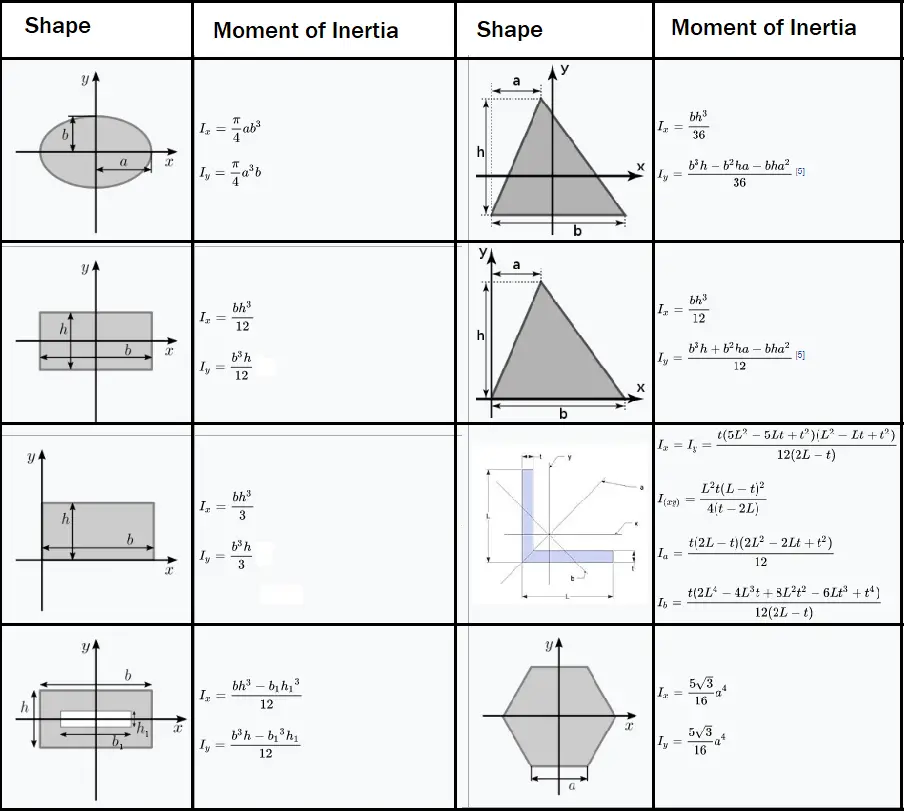
This formula is the most "brute force" approach to calculating the moment of inertia. What is the formula for moment of inertia The formulas are very logical. The moment of inertia can be derived as getting the moment of inertia of the parts and applying the transfer formula: I I 0 + Ad 2. In this section we develop computational techniques for finding the center of mass and moments of inertia of several types of physical objects, using double integrals for a lamina (flat plate) and triple integrals for a three-dimensional object with variable density. A new axis of rotation ends up with a different formula, even if the physical shape of the object remains the same. The moment of inertia of any shape, in respect to an arbitrary, non centroidal axis, can be found if its moment of inertia in respect to a centroidal axis, parallel to the first one, is known. The consequence of this formula is that the same object gets a different moment of inertia value, depending on how it is rotating. Reduced Mass using Moment of Inertia Solution STEP 0: Pre-Calculation Summary Formula Used Reduced Mass Moment of Inertia/ (Bond Length2) I/ (Lbond2) This formula uses 3 Variables Variables Used Reduced Mass - (Measured in Kilogram) - The Reduced Mass is the 'effective' inertial mass appearing in the two-body problem. The formula of Moment of Inertia is expressed as I m i r i2. You do this for all of the particles that make up the rotating object and then add those values together, and that gives the moment of inertia. The formula for the moment of inertia is the sum of the product of mass of each particle with the square of its distance from the axis of the rotation. Basically, for any rotating object, the moment of inertia can be calculated by taking the distance of each particle from the axis of rotation ( r in the equation), squaring that value (that's the r 2 term), and multiplying it times the mass of that particle.


You can calculate the new moment of inertia with the following Steiners theorem: Formula for. The general formula represents the most basic conceptual understanding of the moment of inertia. The Area MOI formula takes into account the geometry of a part and is used to solve related stiffness and deflection formulas. The moment of inertia through the center of mass axis is. The general formula for deriving the moment of inertia.


 0 kommentar(er)
0 kommentar(er)
